
Total force on a particle
Four particles of mass m are arranged in a square of length l, find the total force on one of the particles. Since they all have the same mass and distance, can I just calculate one of the forces and multiple it by 3?
Answer

First, remember that force is a vector and thus has both direction and magnitude, so it's not sufficient to find one force and multiply it because each force points in a different direction. You must add the force vectors individually.
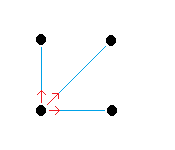
Take a look at this diagram of the situation. Notice that the distance between the masses in opposite corners is greater than the adjacent corners. (Can you figure by how much using geometry?) So there are actually two different distances to use, which means there are two different magnitudes of force to compute.
Try computing the magnitude of the forces between adjacent masses and opposite masses, then adding directions to create the three force vectors (drawn in red on the diagram).
Customer support service by UserEcho


First, remember that force is a vector and thus has both direction and magnitude, so it's not sufficient to find one force and multiply it because each force points in a different direction. You must add the force vectors individually.
Take a look at this diagram of the situation. Notice that the distance between the masses in opposite corners is greater than the adjacent corners. (Can you figure by how much using geometry?) So there are actually two different distances to use, which means there are two different magnitudes of force to compute.
Try computing the magnitude of the forces between adjacent masses and opposite masses, then adding directions to create the three force vectors (drawn in red on the diagram).