
How to find the power dissipated in a simple circuit?
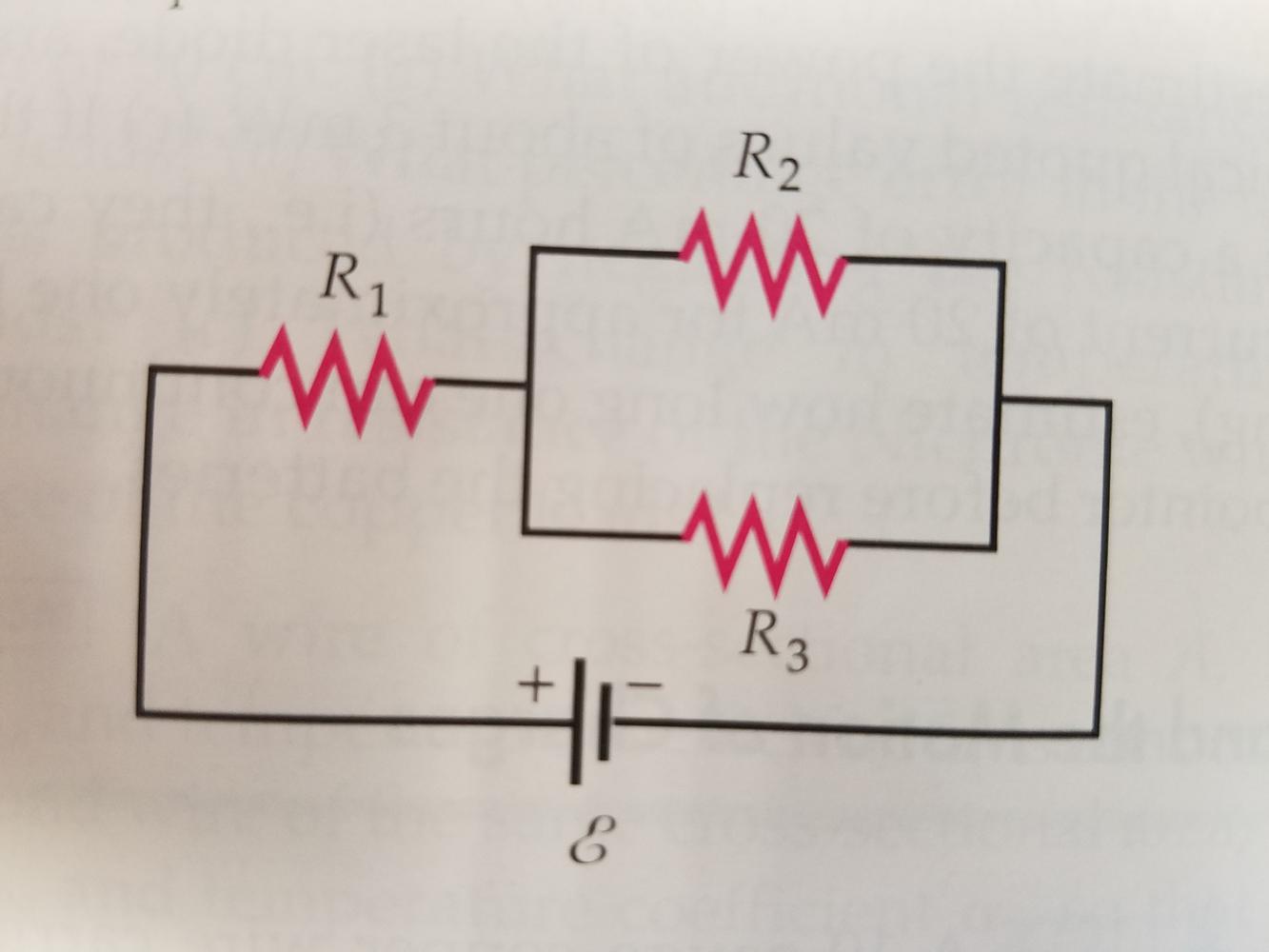
I understand the relationship between power (P) and current (I) and voltage (V). Also, I know the voltages are equally distributed among the resistors if they were all in series, or the current would be equally distributed if they were all in parallel. How do I find the power dissipated (in order to compare them) for each of them when they are set up with this set of resistors? Keep in mind that the resistors are all identical.
Answer

The first thing that you need to do is determine equivalent resistance of the two resistors in parallel (you should be able to easily find how to add resistors in parallel in your textbook). With this, you can determine the voltage drop through both sections, remember that voltages are proportionally distributed to resistors in series and the currents are equal. This should be enough to determine the power dissipated in R1. For R2 and R3, you will have to use the voltage through the equivalent resistor and remember that resistors in parallel must have equal voltage. (Also you mention that you know how P, I, and V relate, but just in case you don't know how R fits in I propose you use incorporate Ohm's law into this relationship).
Customer support service by UserEcho


The first thing that you need to do is determine equivalent resistance of the two resistors in parallel (you should be able to easily find how to add resistors in parallel in your textbook). With this, you can determine the voltage drop through both sections, remember that voltages are proportionally distributed to resistors in series and the currents are equal. This should be enough to determine the power dissipated in R1. For R2 and R3, you will have to use the voltage through the equivalent resistor and remember that resistors in parallel must have equal voltage. (Also you mention that you know how P, I, and V relate, but just in case you don't know how R fits in I propose you use incorporate Ohm's law into this relationship).