
Finding the direction and magnitude of the wind
A plane is flying south at 250 km/h with a wind of unknown speed and direction, but after an hour of flying the plane is 160 km to the southeast. How do I set up this problem in order to solve for the speed and direction of the wind?
Answer

The first thing to do with almost any problem is to draw a diagram. For this problem, the use of cardinal directions tell us that drawing this on a Cartesian plane would be the best fit.
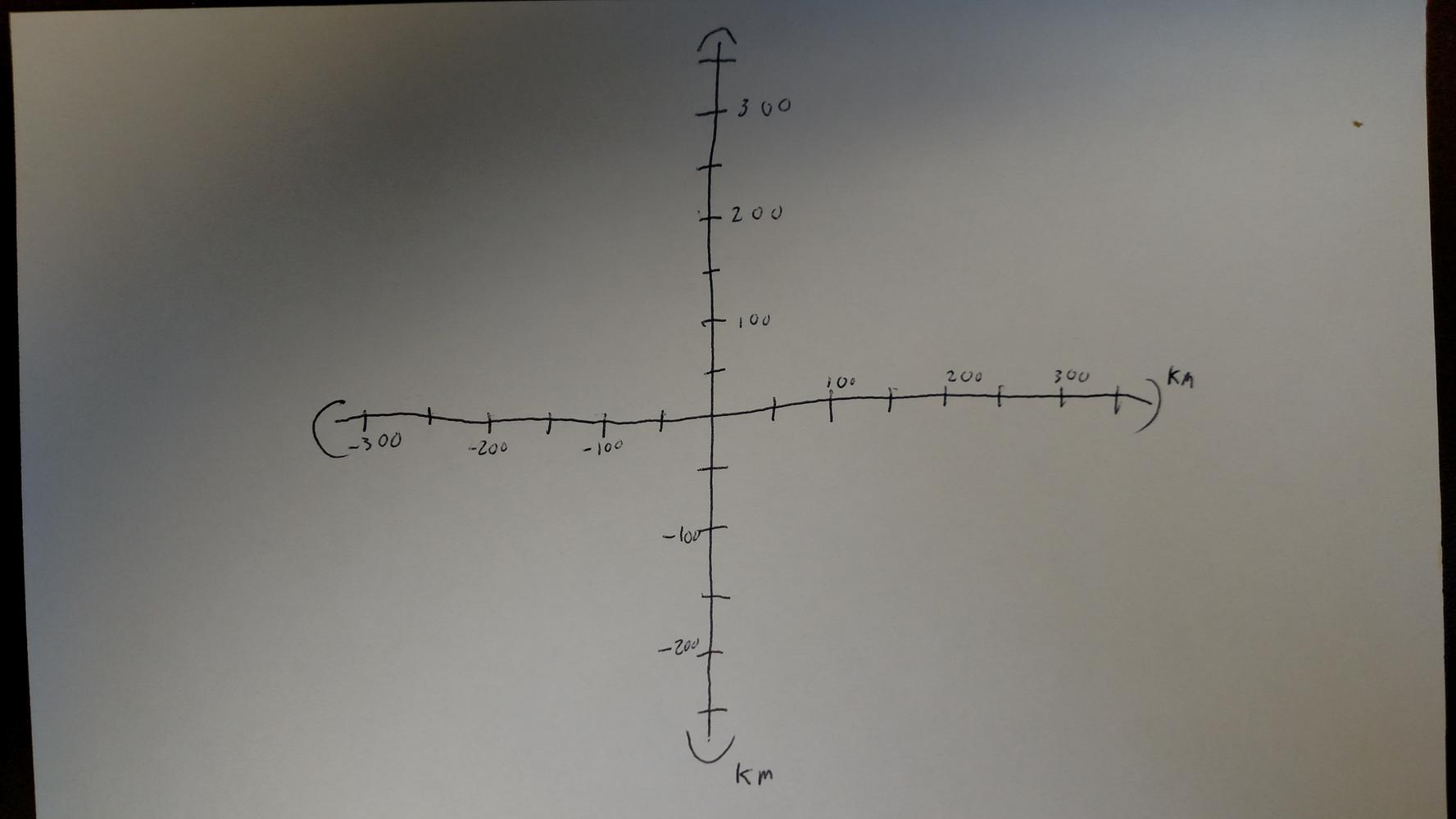
While diagrams do not always have to be to scale, it can often help with the visualization and the fairly normal numbers in this problem allow us an fairly simply scale (remember to put in units!).
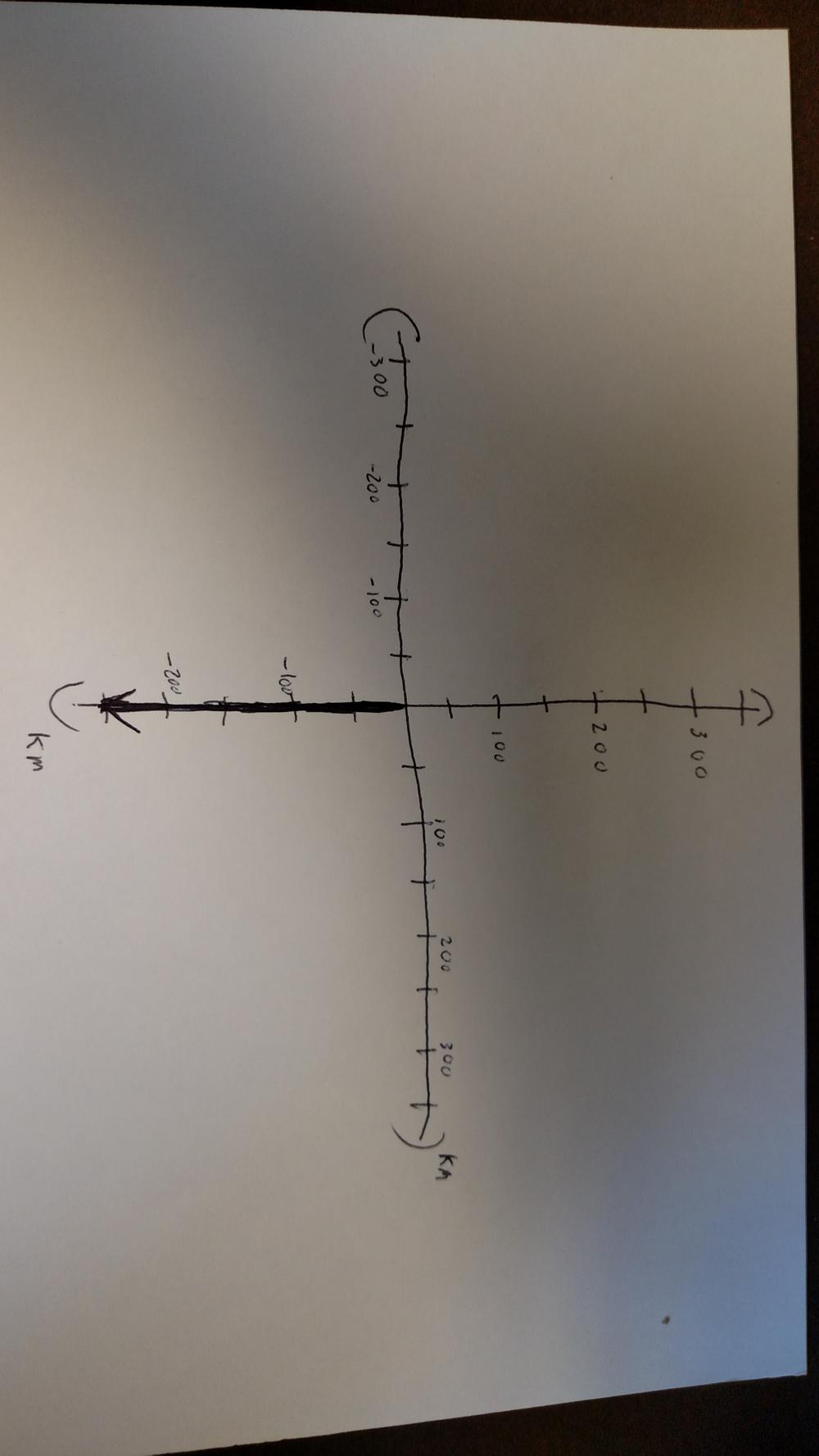
The next step is to simply add each piece of the problem one by one. It is very important to not make any assumptions about the diagram and to simply transcribe only what the problem says. So first we know that the plane was headed due south at 250 km/h, so in one hour the plane should be 250 km south. (Forgive the rotated picture, no matter how I changed the files rotation it would copy in like this)
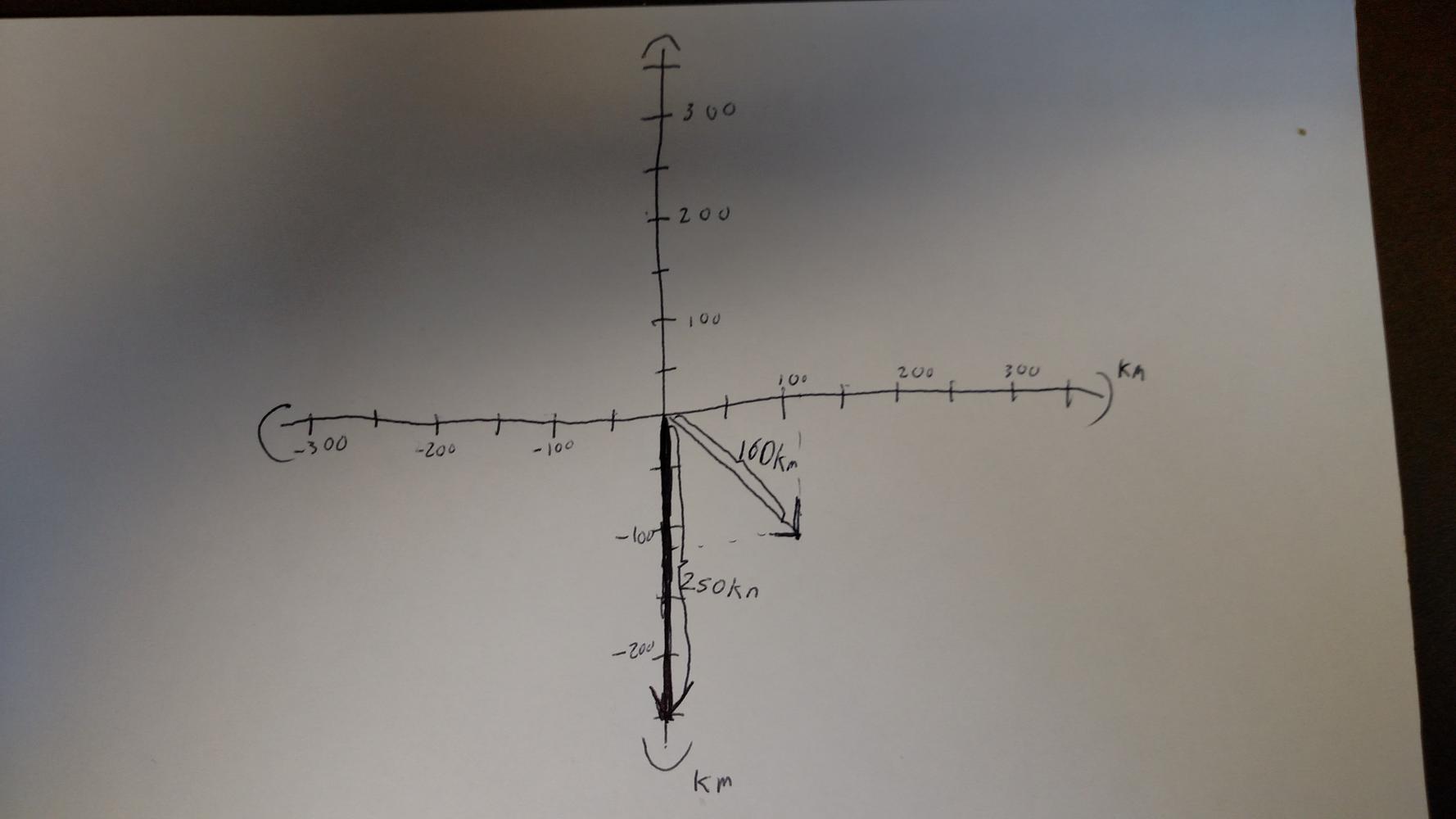
Next we know that the actual distance we covered was 160 km southeast. Here I tried to be a bit meticulous in drawing it and use the x and y components of the distance to keep it to scale. I will leave the exact calculation of these components to you.
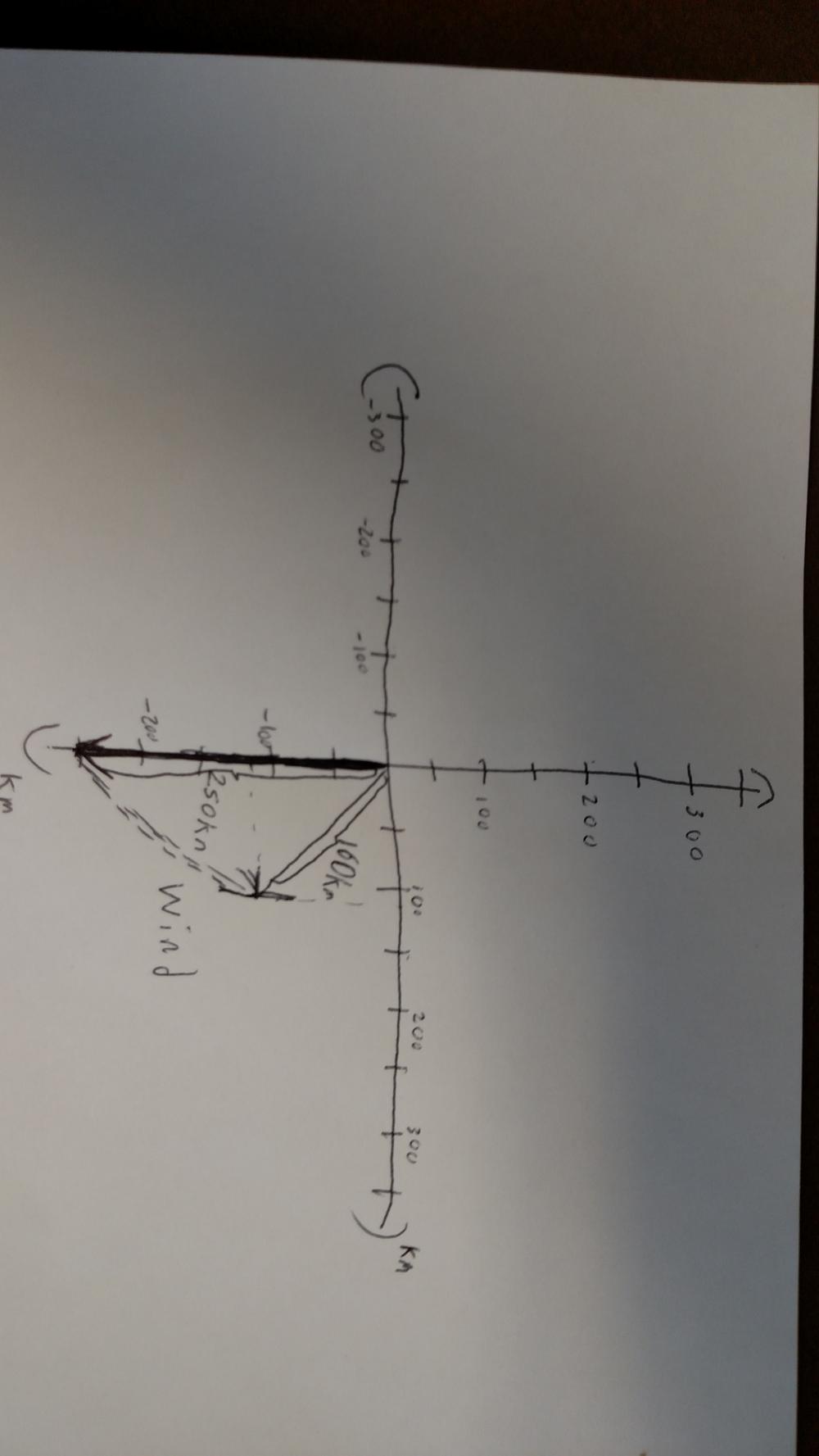
So now we have our expected path and our actual path, but we want to find the strength and direction of the wind that caused this difference. The wind was pushing the plane constantly for the entire hour, so we can draw the distance caused by the wind by drawing a vector from our expected destination to our actual destination.
(If it makes it easy to conceptualize, you can change the displacements into velocities by simply dividing by 1 hour. This way what we are actually solving for is the velocity of the wind that, when added to the velocity caused by the plane, causes the actual velocity)
(Once again ignore the rotation)
From here you have two known vectors and an unknown third that you can create using the two knowns, though be careful on how you create the wind vector from the two known vectors.
Customer support service by UserEcho


The first thing to do with almost any problem is to draw a diagram. For this problem, the use of cardinal directions tell us that drawing this on a Cartesian plane would be the best fit.
While diagrams do not always have to be to scale, it can often help with the visualization and the fairly normal numbers in this problem allow us an fairly simply scale (remember to put in units!).
The next step is to simply add each piece of the problem one by one. It is very important to not make any assumptions about the diagram and to simply transcribe only what the problem says. So first we know that the plane was headed due south at 250 km/h, so in one hour the plane should be 250 km south. (Forgive the rotated picture, no matter how I changed the files rotation it would copy in like this)
Next we know that the actual distance we covered was 160 km southeast. Here I tried to be a bit meticulous in drawing it and use the x and y components of the distance to keep it to scale. I will leave the exact calculation of these components to you.
So now we have our expected path and our actual path, but we want to find the strength and direction of the wind that caused this difference. The wind was pushing the plane constantly for the entire hour, so we can draw the distance caused by the wind by drawing a vector from our expected destination to our actual destination.
(If it makes it easy to conceptualize, you can change the displacements into velocities by simply dividing by 1 hour. This way what we are actually solving for is the velocity of the wind that, when added to the velocity caused by the plane, causes the actual velocity)
(Once again ignore the rotation)
From here you have two known vectors and an unknown third that you can create using the two knowns, though be careful on how you create the wind vector from the two known vectors.